930. Binary Subarrays With Sum - LeetCode Fastest Solution

10 hours ago5 min read

Hello Code Recipian! Today, we'll solve another interesting LeetCode question 930. Binary Subarrays With Sum. This problem has featured in coding interviews at top companies such as Google, Uber and C3 AI.

This article is one of many in our LeetCode problem solutions series—be sure to explore them once you have nailed this one!

Alright, let’s jump straight into the problem statement now.

Problem Statement: 930. Binary Subarrays With Sum

Given a binary array nums and an integer goal, return the number of subarrays with a sum equal to goal.

A subarray is a contiguous part of the given array.

Example 1

Input: nums = [1, 0, 1, 0, 1], goal = 2

Output: 4

Explanation: The nums array has 4 subarrays with sum equal to goal:

[1, 0, 1, 0, 1]

Example 2

Input: nums = [1, 1, 1, 1, 0, 0], goal = 3

Output: 4

Constraints

1 <= nums.length <= 3 * 10^4
nums[i] is either 0 or 1.
0 <= goal <= nums.length

Solution: 930. Binary Subarrays With Sum

Brute Force Approach: A straight forward way to solve this problem is by using the brute force approach. Use two nested loops to iterate through all possible subarrays of the given nums array and count the subarrays whose sum equals goal. However, since this approach relies on nested loops, it has a time complexity of O(n²), making it highly inefficient.

Normal Sliding Window Technique: The standard sliding window technique cannot be applied directly to this problem due to certain constraints in window expansion and contraction, as well as the presence of negative numbers. We have discussed these limitations in 560. Subarray Sum Equals K. To understand this in detail, we recommend going through that article.

Prefix Sum Approach: This problem can be efficiently solved in linear time using the exact prefix sum technique discussed in 560. Subarray Sum Equals K. Although this is a valid and commonly accepted solution in interviews, since we are already familiar with it, we will explore a more innovative and insightful solution!

Modified Sliding Window Approach: We know that the given array consists of only 0s, 1s and does not contain negative numbers. We can use this fact to our advantage, and apply the modified sliding window to solve this problem in linear time. In this approach, we first use the sliding window to calculate the count of subarrays with a sum at most equal to the goal. Then, we apply the sliding window again to calculate the count of subarrays with a sum at most equal to goal - 1. Using these two counts, we can determine the number of subarrays with a sum exactly equal to the goal using the formula:

Count of subarrays with sum equal to goal = Count of subarrays with sum at most goal - Count of subarrays with sum at most (goal - 1)

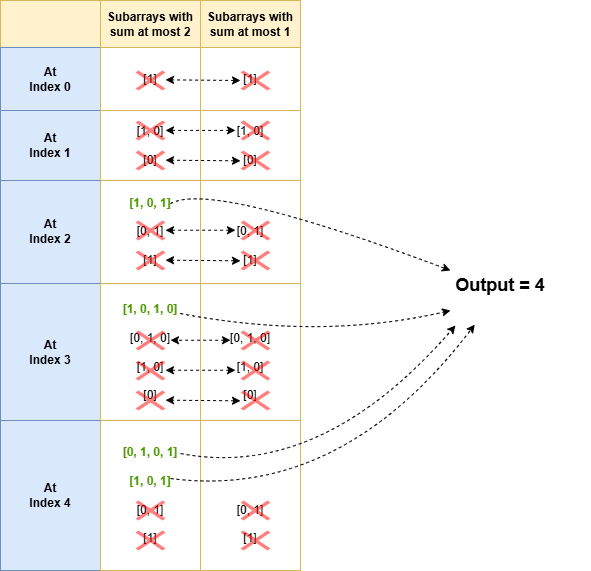
The intuition behind this approach is that, when we subtract count of subarrays with sum at-most goal - 1 from count of subarrays with sum at most goal, all the common subarrays from both cancel each other out, and we will be left with only the subarrays whose sum is equal to goal.

Note: This approach only works if the given input consists of non-negative numbers.

Let's understand this with an example. Consider the given array nums= [1, 0, 1, 0, 1] and goal = 2. Below is the list of subarrays for sum at most 2 and at most 1 at each index in nums:

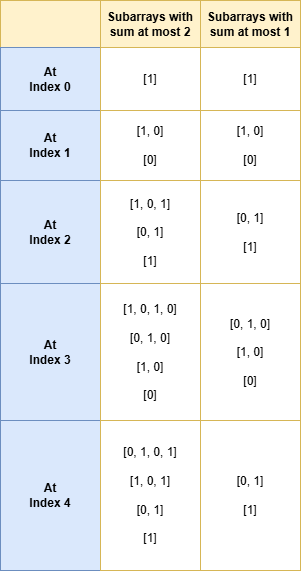
By subtracting these two counts, the common subarrays cancel out, leaving only the count of subarrays whose sum equals 2, as illustrated in the diagram below.

Image showing how common subarrays with sum 2 and 1 cancel out each other

Algorithm

The solution is implemented in two parts.

Part 1:
Define the function countSubarraySumAtMostK(), which calculates the number of subarrays with a sum at most k.
Part 2:
Call countSubarraySumAtMostK() twice:
1. First, to count subarrays with a sum at most goal.
2. Second, to count subarrays with a sum at most goal - 1.
3. The final result is obtained by subtracting the second count from the first.

Implementing countSubarraySumAtMostK():

Initialization: Initialize four variables: start, end, sum and count.
1. start, end track the boundaries of the sliding window. Both start at index 0.
2. sum keeps track of the current window's sum while we iterate through the nums array.
3. count is used to store result, total number of valid subarrays with sum equal to goal.
Counting subarrays with sum at most K:
Iterate trough the nums array from start to finish. In each iteration perform the following steps:
1. Expand the window by adding the current element to sum.
2. If sum exceeds k, shrink the window by removing elements from start until sum becomes equal to k.
3. Since sum is now at most k, count all valid subarrays ending at end. This count is given by the formula: count = end - start + 1.
Returning the final count: Once the iteration through nums array is complete, return the value of count as final result.

How does the formula end - start + 1 for counting subarrays work?

All subarrays that end at end and start anywhere between start and end. These subarrays are valid because their sum is always ≤ goal, as we ensure this by expanding and shrinking the window before applying the formula.

The number of such subarrays at index end is end - start + 1.

The formula works because, the subarrays that satisfy this condition are

[nums[start]], [nums[start], nums[start+1]], ..., [nums[start],...,nums[end]]. Their count is simply end - start + 1.

Since there are exactly (end - start + 1) such subarrays, adding this value to count ensures we correctly count all subarrays ending at end that have a sum ≤ goal.

Want to master coding? Looking to upskill and crack interviews? We suggest you check out these specially designed courses:

Simulation

The following diagram visually illustrates how the algorithm works:

Code

Go Solution

Python Solution

Java Solution

JavaScript Solution

TypeScript Solution

C++ Solution

C# Solution

C Solution

PHP Solution

Kotlin Solution

Swift Solution

Ruby Solution

Scala Solution

Rust Solution

Dart Solution

Racket Solution

Complexity Analysis

Time Complexity

Helper function countSubarraySumAtMostK():

The helper function processes each element in nums at most twice—once when the end pointer expands the window and once when the start pointer shrinks it. As a result, the time complexity is O(n) + O(n) = O(n).

Main function numSubarraysWithSum():

The main function invokes the helper function twice: once for subarray sum at most goal and once for subarray sum at most goal - 1. Each call takes O(n) time, as explained above.

Thus, the overall time complexity of the solution is O(n) + O(n) = O(n).

Space Complexity

The algorithm uses a constant amount of extra space for variables like start, sum, end etc., regardless of the input size. Therefore space complexity of this algorithm is O(1).

Want to learn more about the prefix sum pattern? Explore our other articles on this topic:

100% FREE for a Limited Time!: Enjoy Expert Tutorials, Pro Tips, and Exclusive Resources at ZERO Cost! For a limited time enjoy 100% discount on the Code Recipe Membership Plan. Sign up now and get access to exclusive premium content for free. Hurry—claim your FREE access before the timer runs out! - Claim now.