5 days ago3 min read

GeeksforGeeks - Maximum Sum Subarray of Size K

Updated: 21 hours ago

Hello Code Recipian! Welcome back to another article on coding questions. Today we will be solving GeeksForGeeks problem, Maximum Sum Subarray of Size K.

Problem Statement: Maximum Sum Subarray of Size K

Given an array of positive numbers and a positive number 'k', find the maximum sum of any contiguous subarray of size 'k'.

Example 1:

Input: arr = [2, 1, 5, 1, 3, 2], k=3 
Output: 9
Explanation: Subarray with maximum sum is [5, 1, 3].

Example 2:

Input: arr = [2, 3, 4, 1, 5], k=2 
Output: 7
Explanation: Subarray with maximum sum is [3, 4].

Solution

This is a classical sliding window technique problem. If you are new to sliding window concept, we would suggest you to go through this article on sliding window concept before you proceed further in this article.

Algorithm

Below is the step by step explanation for this algorithm:

Initialization:
Initialize two variables maxSum and windowSum. Both maxSum and windowSum are initially set to 0.
1. maxSum is used to store the maximum subarray sum found so far.
2. windowSum is used to store the subarray sum for the current window.
Calculate the subarray sum for the first window:
Loop through the first k elements of array arr and calculate its sum. This initial window sum forms the basis on which we further build our algorithm.
Update maxSum:
Since this is the first subarray sum, we update maxSum with the current windowSum.
Slide the window:
Now for each iteration, slide the window to right by one element and perform the following operations:
1. Remove (subtract) the previous array element from the windowSum.
2. Add the current element to windowSum.
3. If current windowSum is greater than maxSum, update maxSum with current windowSum.
Return the result:
Once sliding window reaches the end of array, return the final value in maxSum as result.

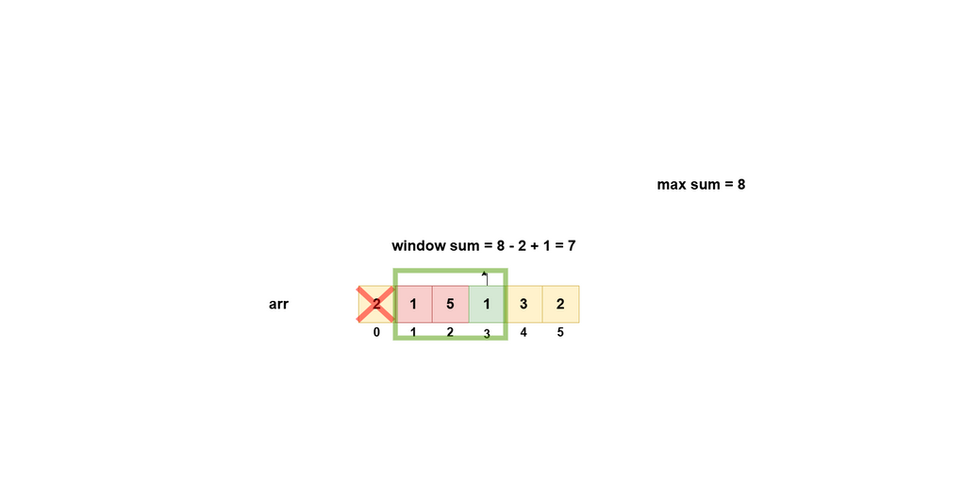
Simulation

Below diagram shows a pictorial depiction of the working of this algorithm:

Want to master coding? Looking to upskill and crack interviews? We suggest you check out these specially designed courses:

Code

Go Solution

Python Solution

Java Solution

JavaScript Solution

C++ Solution

C# Solution

PHP Solution

Kotlin Solution

Swift Solution

Ruby Solution

Complexity Analysis

Time Complexity

Calculating first subarray sum:

In the first loop, we calculate the sum of the first subarray window by iterating from index 0 to kth index. This has a time complexity of O(k).

Sliding the window for the remaining subarrays:

For calculating the window sum of remaining subarrays, we iterate arr from 1st index to (n-1)th index (n-k elements in total). This has a time complexity of O(n-k).

Therefore the overall time complexity of this algorithm is O(k) + O(n-k) = O(n).

Space Complexity

Apart from maxSum and windowSum variables, this algorithm does not use any extra space for its computation. Therefore, the space complexity of this algorithm is O(1).

That brings us to the end of this article. We sincerely appreciate the time you have taken to read through it. If there are any questions, feel free to ask them in the comments below. We're here to help and will gladly answer your queries.

If you enjoyed this article, please subscribe to our website and Youtube channel. Your support inspires us to create more such articles in the future.

Don't forget to delve into more such fascinating articles from Code Recipe in our blogs section. There's a wealth of knowledge waiting for you there!

Code Recipe Limited Time Offer: Get 100% discount on Code Recipe Membership Plan. Join now and get exclusive access to premium content for free. Hurry! Offer only available for a limited time - Join now.

Follow us: YouTube, Facebook, Twitter, LinkedIn, Tumblr, Instagram.