112. Path Sum - LeetCode Fastest Solution

Hello Code Recipian! Welcome back to another article on LeetCode problem solutions. Today we will be solving LeetCode problem on binary tree 112. Path Sum. Getting a good understanding of this problem will help you solve advanced level tree questions like 113. Path Sum II.

Let's check out the problem statement.

Problem Statement: Path Sum

Given the root node of a binary tree and an integer targetSum, return true if the tree has a path from root-to-leaf such that, sum of all node values along the path equals targetSum. Return false otherwise.

A node in a tree is called a leaf node, if it has no children.

Example 1:

Input: root = [5, 4, 8, 11, null, 13, 4, 7, 2, null, null, null, 1], targetSum = 22

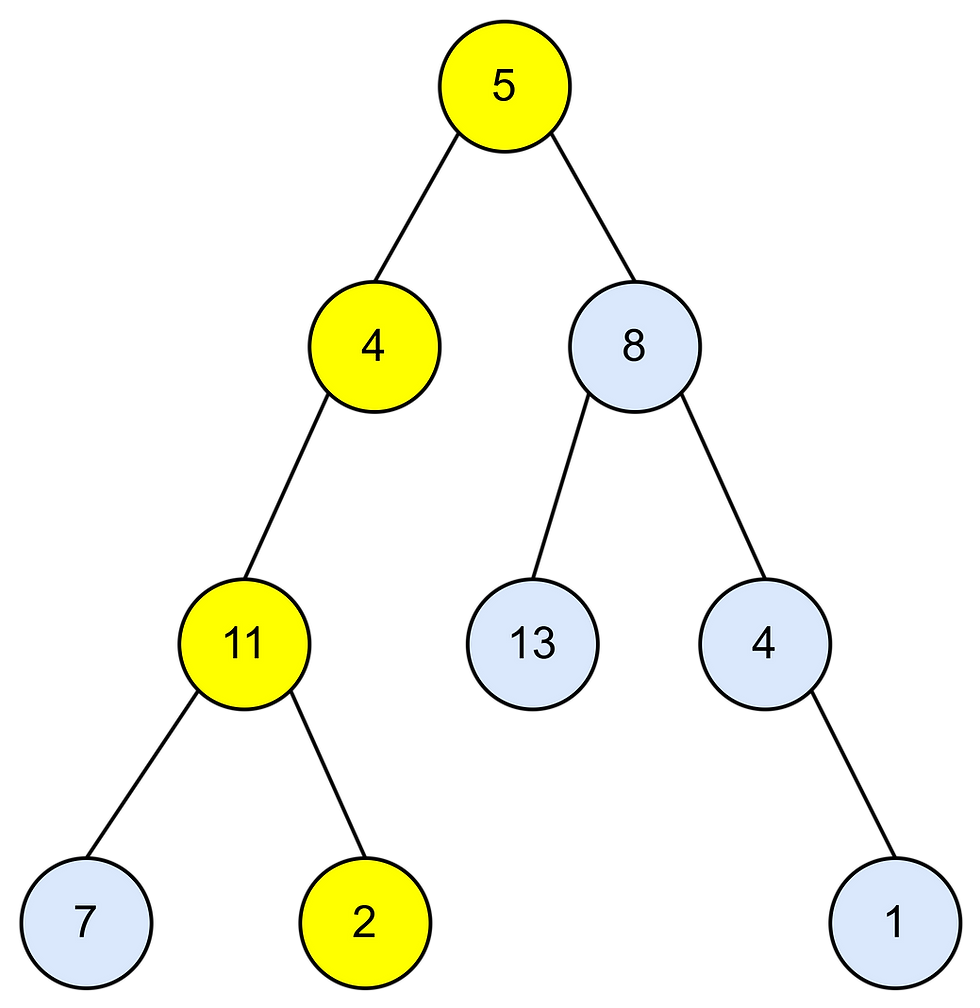
Output: true Explanation: Node values in the path highlighted in yellow add up to targetSum.

Example 2:

Input: root = [5, 4, 8, 11, 2, 10, 4], targetSum = 23

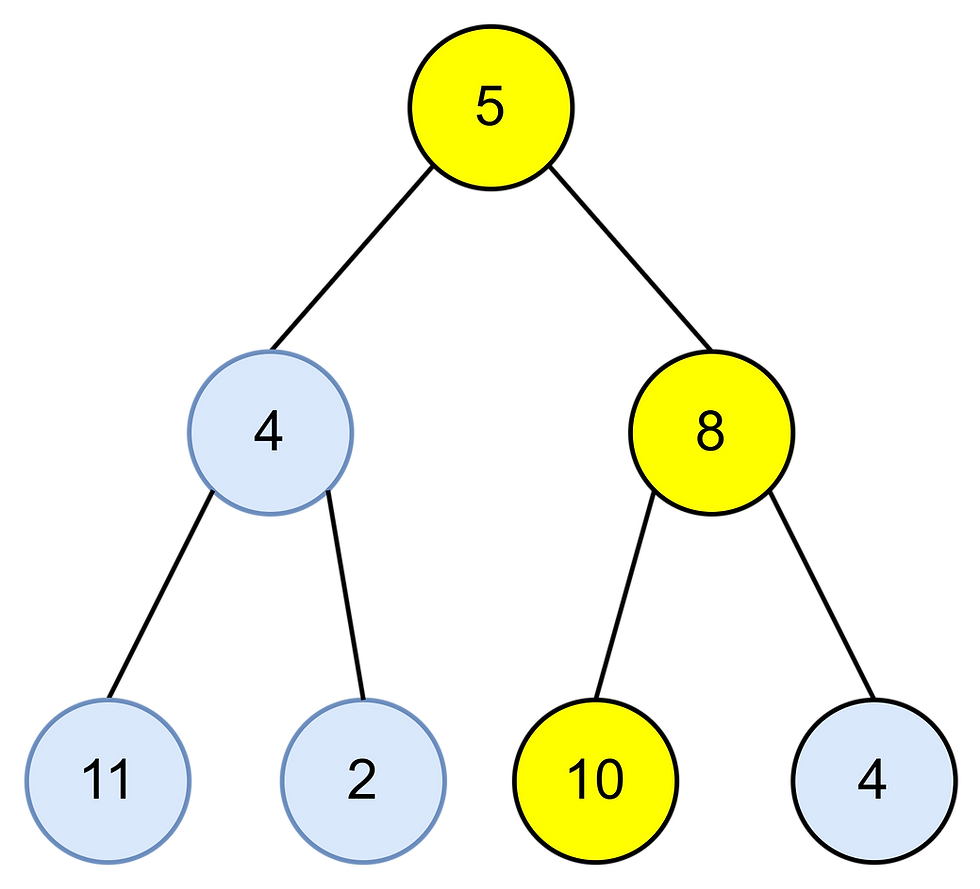
Output: true

Constraints:

• The number of nodes in the tree is in the range [0, 5000].

• -1000 <= Node.val <= 1000

• -1000 <= targetSum <= 1000

Solution

In this problem we are given a binary tree, we need to find the sum of any path originating from root to leaf node, whose node values add up to the given targetSum.

In this article we will be discussing how we can solve this problem optimally using the depth first search traversal approach. The idea is to use recursion and perform depth first search (DFS) of the given binary tree.

We traverse every root-to-leaf path in the given tree and in each step, we subtract the current node value from the given target sum. When we reach the leaf node, we check if the current sum value is zero in order to determine if the current path adds up to the given target sum.

Let's see how this algorithm works in detail.

Algorithm

Below is a step-by-step explanation for the working of the algorithm:

1. Base Case:

   We will be using recursion to perform depth first search of the given binary tree. Every recursive solution must have a base case to indicate when the recursion must stop. In our case, the base case is when we reach a null node. If we reach a null node, we stop and return false.

2. Subtract current node from targetSum:

   In each recursive call we subtract the current node value from targetSum. The logic behind this is that, if there exists a root-to-leaf path that adds up to the given targetSum, as we subtract current node values from targetSum, when we reach the leaf node the targetSum value must become 0. If targetSum does not become zero when we reach leaf the node, it means that the current path sum does not add up to the given targetSum.

3. Verify if path sum is possible:

   This is the part where we validate if the current path from root to leaf adds up to the given targetSum. We can verify this by checking if the following two conditions are satisfied:

   1. Current node is a leaf node and,

   2. targetSum after subtraction must have reached 0.

   If either of the a or b is not satisfied, we continue our DFS. If both conditions are satisfied, it means we have found a root-to-leaf path whose sum is equal to targetSum. Therefore, we return result as true.

4. Recursive DFS calls:

   Final part is to define the recursive calls for DFS, one call for the left child and one for the right child.

   1. If either of these recursive calls return true, it means a valid root-to-leaf path with targetSum exists, so we return true.

   2. If both these calls return false, it means no such path exists, so we return false.

Simulation

Below diagram shows a pictorial depiction for the working of the algorithm:

Want to master coding? Looking to upskill and crack interviews? We suggest you check out these specially designed courses:

1. Udemy Video Tutorials - Available at 95% off

2. System Design Interview Complete Guide

3. Cracking The Coding Interview - Most Preferred Book For Coding Interviews

4. Data Structures And Algorithms - A Complete Guide 

5. Learn In-Demand Tech Skills And Stay Ahead Of Others

Code

Go Solution

Python Solution

Java Solution

JavaScript Solution

TypeScript Solution

C++ Solution

C# Solution

C Solution

PHP Solution

Kotlin Solution

Swift Solution

Ruby Solution

Scala Solution

Rust Solution

Complexity Analysis

Time Complexity

If n is the number of nodes in the given binary tree, time complexity of this algorithm is O(n), because in the worst case, we end up traversing every node in the binary tree once to arrive at the result. The worst case occurs when the the given tree is a skewed binary tree.

Space Complexity

This algorithm does not use any additional variables that have impact on space complexity. However, because we are using recursion here, the space complexity of this algorithm is O(n) for the recursion call stack.

That brings us to the end of this article. We appreciate the time you have taken to read through it. If you have any questions, feel free to ask them in the comments below. We're here to help and will gladly answer your queries.

If you enjoyed this article, please subscribe to our website and Youtube channel. Your support inspires us to bring out more such articles in future.

Don't forget to delve into more such fascinating articles from Code Recipe in our blogs section. There's a wealth of knowledge waiting for you there!

Code Recipe Limited Time Offer: Get 100% discount on Code Recipe Membership Plan. Join now and get exclusive access to premium content for free. Hurry! Offer only available for a limited time - Join now.

Follow us: YouTube, Facebook, Twitter, LinkedIn, Tumblr, Instagram.