Coding Patterns - Prefix Sum Pattern

1 day ago5 min read

Hello Code Recipian, we come back! We are launching a new series on Coding Patterns and this article marks the first in the series.

What are Coding Patterns?

A coding pattern refers to a common approach or technique used to solve a specific category of coding questions. A strong understanding of coding patterns and ability to recognize patterns quickly, can make solving coding questions a lot more easier, particularly in coding interviews.

Prefix Sum Pattern

Prefix sum is an efficient and powerful technique, often useful in coding interviews and competitive coding. A prefix sum is the combined sum of all elements till the current index. Example, for array arr = [1, 2, 3, 4],

Prefix sum at index 0 = 1
Prefix sum at index 1 = 1 + 2 = 3
Prefix sum at index 2 = 1 + 2 + 3 = 6
Prefix sum at index 3 = 1 + 2 + 3 + 4 = 10

For a given array arr, a prefix sum array is a new array formed by summing up all the elements upto a specific index, and this is done for every index in arr.

For example, consider the array arr = [1, 2, 3, 4]. The prefix sum array for arr is prefixSum = [1, 3, 6, 10]. Here each element in prefixSum array is a sum of all elements from the beginning of arr array to the current index.

How is Prefix Sum Useful?

Prefix sum provides an efficient way preprocess and query cumulative information about arrays and sequences. Once the prefix sum array is formed (takes O(n) time), it allows us to solve a variety of problems in linear time which might otherwise require complex or inefficient solutions.

Range Sum Query using Prefix Sum

Let us consider one such application of prefix sum pattern, "Finding the Range Sum". Having a pre-computed prefix sum array allows us to get the sum of a range of elements (sum of any subarray) in the given array in O(1) time. Let's see how we can do this.

If start is the starting index of a range and end is the ending index. The range sum of arr from start to end can be calculated using the formula:

Range Sum(start, end) = prefixSum[end] - prefixSum[start - 1]

If the range starts from first element, i.e. if start = 0 then,

Range Sum(0, end) = prefixSum[end]

Algorithm: Range Sum Query using Prefix Sum

Below is a detailed explanation for the working of the algorithm:

Initialization:
1. Consider arr is the given input array having size n. Create a new array prefixSum of same size n.
2. Initially the prefixSum array is empty (or initialized default values).
Construct prefix sum array:
1. Assign the first element of arr to prefixSum[0] (since there are no elements before index 0 to calculate prefix sum).
2. Iterate through the given input array arr from index 1 to n-1.
3. In each iteration calculate the prefix sum at the current index. The prefix sum at the current index i can be calculated by adding the current element to the prefix sum at index i-1 (previous prefix sum), i.e. prefixSum[i] = prefixSum[i-1] + arr[i].
4. Repeat step c and and calculate the prefix sum at all indices from 1 to n.
Get range sum:
1. Once the prefix sum array is constructed, we can get the subarray sum of any range from 0 to n in arr.
2. Use the appropriate range sum formula described earlier for calculating range sum:
  Range Sum (start, end) = prefixSum[end] - prefixSum[start - 1]
  or
  Range Sum (0, end) = prefixSum[end]

Want to master coding? Looking to upskill and crack interviews? We suggest you check out these specially designed courses:

Simulation

Let's understand this algorithm with an example. Consider arr = [1, 2, 3, 4, 5, 6] is the given array.

We are asked to find the range sum from index 2 to 5.

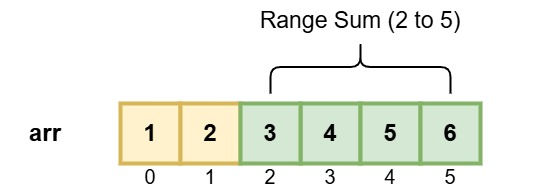
First we construct the prefix sum array using the formula prefixSum[i] = prefixSum[i-1] + arr[i]. After applying this formula for every index from 0 to n, our final prefixSum array for arr will be as shown below:

Next use the range sum formula for getting the range sum from 2 to 5:

Image showing how range sum is calculated

As you can see from above diagram range sum from 2 to 5 is equal to 21, which is the sum of elements at indices 2 to 5, i.e. elements [3, 4, 5, 6].

Below is a pictorial depiction of how the range sum formula works in general:

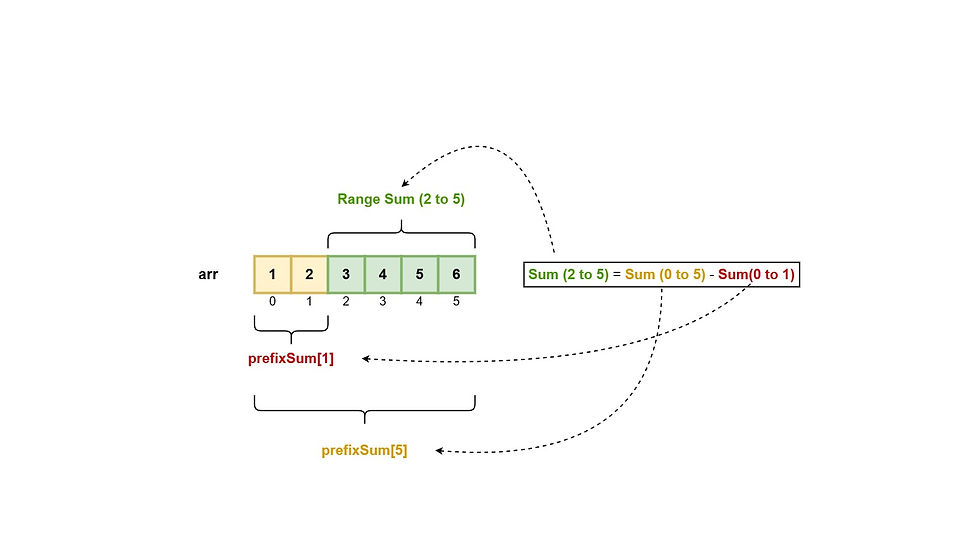
Image showing the general working of range sum calculation using prefix sum

As you can see from the above diagram, when the sum of elements before the start index of a range is subtracted from the sum of all elements till the last range index, this will effectively give us the difference between two sums, which is nothing but the range sum from start to end. This is the intuition behind using this formula for calculating the range sum.

Code

Go

Python

Java

JavaScript

TypeScript

C

C++

C#

PHP

Kotlin

Swift

Ruby

Scala

Rust

Complexity Analysis

Time Complexity

Constructing prefix sum array:

We must traverse every element in the given array arr once in order to construct prefixSum array. Time complexity for this step is O(n).

Getting range sum or subarray sum:

Once the prefix sum array is available, we can get the range sum directly using the range sum formula. This takes constant time, so time complexity for this step is O(1).

Overall time complexity:

Combining the above two steps, the overall time complexity for getting the range sum/subarray sum using the prefix sum technique is O(n) + O(1) = O(n).

Space Complexity

This pattern uses the an additional array prefixSum for storing prefix sums for each index in arr. Hence the space complexity for prefix sum pattern is O(n).

Other Applications of Prefix Sum

Apart from range sum range calculation, prefix sum pattern is also used in several other use cases. Few are described below:

Finding sum of subarrays.
Counting subarrays with specific properties (like subarrays with given sum, subarrays divisible by k etc.).
Optimizing sliding window problems.
2D prefix sum problems.

Conclusion

The prefix sum pattern helps us simplify and optimize a diverse range of coding problems. By pre-computing prefix sums we can bring down the time complexity of problems like range queries, subarray sum problems from quadratic time to linear time. Mastering this pattern is essential for competitive programming and technical interviews.

We hope this article has helped you build a solid understanding of the prefix sum pattern. In the upcoming articles we will solve several problems using this pattern. Subscribe to Code Recipe and stay tuned for more!

Code Recipe Limited Time Offer: Enjoy a 100% discount on the Code Recipe Membership Plan. Sign up now and get access to exclusive premium content for free. Act fast—offer only available for a limited time - Join now.